Os logaritmos, uma ferramenta matemática poderosa, surgiram da necessidade de simplificar cálculos complexos, especialmente em áreas como a astronomia e a navegação. Sua invenção revolucionou a forma como cientistas e matemáticos abordavam problemas que envolviam grandes números e operações tediosas.

História e Evolução

A história dos logaritmos começa no início do século XVII, com o matemático escocês John Napier. Em 1614, Napier publicou “Mirifici Logarithmorum Canonis Descriptio”, onde apresentou uma nova abordagem para simplificar multiplicações e divisões, transformando-as em somas e subtrações, respectivamente. Sua principal motivação era agilizar os cálculos astronômicos, que eram extremamente trabalhosos na época.

Embora Napier tenha introduzido a ideia, foi o matemático inglês Henry Briggs quem realizou ajustes significativos no conceito. Briggs propôs o uso da base 10 para os logaritmos, o que facilitou ainda mais os cálculos e levou à criação das populares tabelas de logaritmos decimais. Essas tabelas foram amplamente utilizadas por cientistas e engenheiros nos séculos XVII e XVIII para resolver equações e realizar diversos cálculos.

A importância dos logaritmos se expandiu rapidamente. Na astronomia, eles simplificaram cálculos de movimentos planetários e posições celestes. Na engenharia, auxiliaram na construção de máquinas e edifícios, e na matemática financeira, permitiram o cálculo mais rápido de juros compostos. Os logaritmos também foram cruciais para o desenvolvimento do cálculo, simplificando equações exponenciais e funções complexas.

Mesmo com o avanço da tecnologia e o advento das calculadoras, os logaritmos continuam sendo uma ferramenta fundamental na matemática moderna, ciência e tecnologia. O logaritmo natural (base e) é essencial para o cálculo e análise matemática, com aplicações em física e biologia. Na informática, são usados para medir a complexidade de algoritmos, e na economia, para modelar crescimento e decaimento exponenciais.

Aplicações em Outras Áreas do Conhecimento

Os logaritmos transcendem a matemática pura, sendo aplicados em diversas áreas:

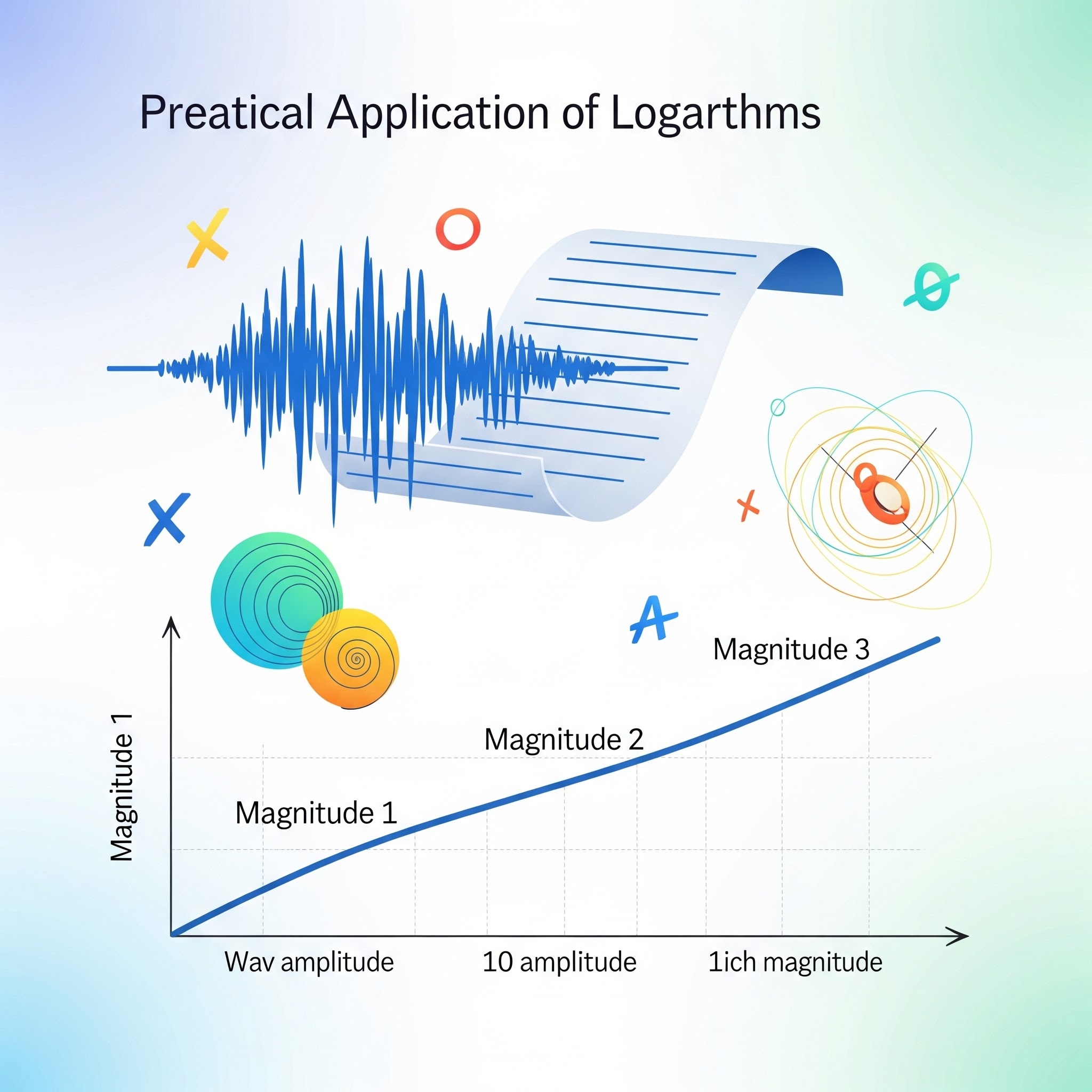
• Física e Engenharia: Utilizados em escalas logarítmicas para medir intensidades, como a escala Richter (terremotos), decibéis (som) e pH (acidez/alcalinidade). Também são empregados em cálculos de decaimento radioativo e crescimento populacional.
• Biologia: Modelagem de crescimento de populações de bactérias e vírus, e em estudos de farmacocinética.
• Economia e Finanças: Cálculos de juros compostos, crescimento de investimentos e análise de dados financeiros.
• Informática: Análise da complexidade de algoritmos e em estruturas de dados.
• Música: A relação entre a altura e a frequência das notas musicais é logarítmica.

Incidência em Exames (ENEM, FUVEST, UNICAMP, UNESP) nos Últimos 4 Anos

Os logaritmos são um tema recorrente nos principais exames vestibulares do Brasil, sendo cobrados de diferentes formas. Abaixo, detalhamos a incidência nos últimos 4 anos, com base nas informações disponíveis:

• ENEM (Exame Nacional do Ensino Médio): Logaritmos são frequentemente abordados em questões contextualizadas, que exigem a interpretação de gráficos, tabelas e situações-problema do cotidiano. É comum encontrar questões que envolvem escalas logarítmicas, como a Richter para terremotos, ou problemas de crescimento e decaimento exponencial. A prova valoriza a aplicação da matemática em cenários reais, e os logaritmos são uma ferramenta essencial para isso. Questões que envolvem logaritmos foram identificadas em edições recentes, como 2023, 2020, 2018, 2017 e 2016.
• FUVEST: A FUVEST costuma cobrar logaritmos no contexto de funções, especialmente a função logarítmica. As questões podem envolver a análise de gráficos de funções logarítmicas, propriedades dos logaritmos e a resolução de equações e inequações logarítmicas. Logaritmos representam cerca de 6,40% dos temas de Matemática na primeira fase da FUVEST. Uma questão envolvendo função logarítmica foi observada na FUVEST 2023.
• UNICAMP: A UNICAMP, assim como a FUVEST, também aborda os logaritmos em um contexto mais analítico, frequentemente em questões que envolvem funções exponenciais e logarítmicas. A compreensão da definição de logaritmo e suas propriedades é fundamental para um bom desempenho. A análise de incidência nos últimos 12 anos indica que funções, incluindo logarítmicas, são um tema com alta recorrência.
• UNESP: A UNESP apresenta questões de logaritmos que podem variar de aplicações diretas das propriedades a problemas contextualizados. A compreensão da definição de logaritmo e suas propriedades é fundamental para um bom desempenho. Logaritmos e exponenciais juntos representam cerca de 8,8% dos temas de Matemática na UNESP.

Em resumo, o estudo dos logaritmos é crucial para os estudantes que almejam o ensino superior, não apenas pela sua relevância histórica e suas amplas aplicações em diversas áreas do conhecimento, mas também pela sua constante presença nos exames vestibulares mais importantes do país.